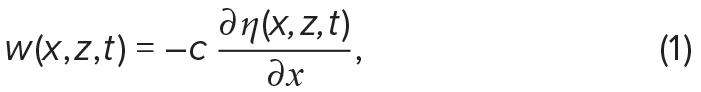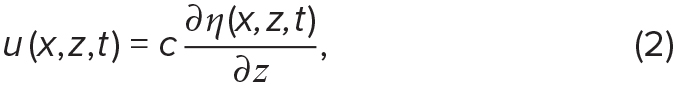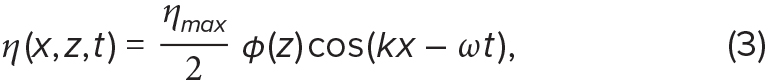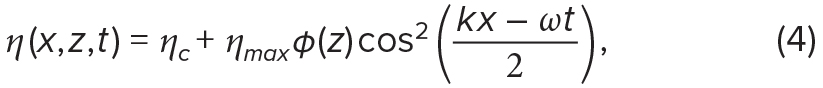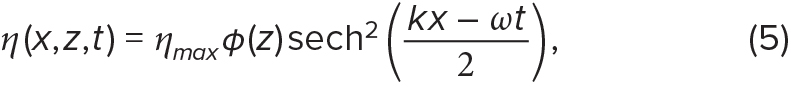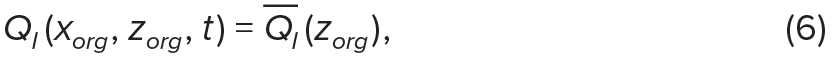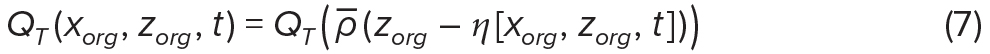Linear and nonlinear internal waves are widespread phenomena with important implications for the ocean’s ecology. Here, we review the biological impacts of non-breaking internal waves for three broad categories of organisms: sessile organisms, passive plankton, and depth-keeping plankton. We use heuristic simulations to contrast the effects of passing internal waves for each of these groups. In the case of irradiance, an isobaric quantity, light availability is only modulated for passive plankton. Wave-induced horizontal transport enhances this effect, because transport in the direction of wave propagation implies that passive plankton spend longer within each wave. This is true for both linear waves, where horizontal transport is due exclusively to Stokes drift, as well as for weakly nonlinear waves, where transport arises from both nonlinearity and Stokes drift. In the case of depth-keeping plankton, a similar effect is seen for isopycnal properties. In a simple example, where we set the vertical distribution of temperature to match that of density, wave-induced horizontal transport alters the overall water temperatures depth-keeping plankton are exposed to. These results emphasize that horizontal transport within internal waves is not only important to dispersal but also modulates the effects of wave-induced vertical disturbances on plankton.

Phytoplankton bloom (Tetraselmis spp.) off La Jolla, California. Photo credit: Eddie Kisfaludy. > High res figure

Introduction

Internal waves modulate the local environment of coastal marine organisms in numerous ways. They can inject nutrients into the euphotic zone (Sandstrom and Elliott, 1984; Lucas et al., 2011), they can displace phytoplankton vertically and affect the solar irradiance they are exposed to (Kamykowski, 1974; Holloway and Denman, 1989; Evans et al., 2008), they can concentrate vertically swimming plankton and transport them (Zeldis and Jillett, 1982; Shanks, 1983; Franks, 1997; Lennert-Cody and Franks, 1999; Pineda, 1999), they can dampen thermal stress and provide nutrients to coral reefs (Leichter et al., 2003; Wall et al., 2015), and they can bring hypoxic deep water to shallow benthic environments (Booth et al., 2012; Walter et al., 2014).

Here, we limit our scope to the biological impacts of non-breaking internal waves. These waves displace isopycnals vertically as they propagate, inducing vertical and horizontal currents but only little mixing between waters of different densities. While fluid properties such as temperature or nutrient concentrations can change slowly in time due to mixing, buoyant fluxes, and biological activity, they generally follow isopycnals. Thus, passing internal waves change the environment of marine organisms by deforming the vertical distribution of fluid properties. For marine organisms anchored to a substrate, internal waves pass by at their propagation speed c. For marine organisms that drift with ocean currents, however, both wave-induced and background currents can cause the relative propagation speed of the wave to be faster or slower, so the drifting organisms are exposed to internal wave troughs or crests for longer time periods than are stationary organisms.

Prior studies have quantified wave-​induced total horizontal transport for water parcels and both neutrally buoyant and vertically swimming plankton (e.g., Inall et al., 2001; Shroyer et al., 2010; Zhang et al., 2015; Franks et al., 2020; Garwood et al., 2020). However, to our knowledge, no studies have investigated how horizontal drift in an internal wave can change the overall exposure of plankton to various environmental properties. Throughout this manuscript, we consider three categories of marine organisms: (1) those, such as coral reefs, that are anchored to a substrate and are not moved by internal waves, (2) planktonic organisms, such as non-swimming phytoplankton, that are moved by internal wave velocities both horizontally and vertically, and (3) planktonic organisms, such as strong swimming larvae, that are moved horizontally by internal wave velocities but that perfectly oppose wave vertical velocities in order to maintain a fixed depth (Figure 1). We refer to these organisms as “sessile,” “passive,” and “depth-keeping,” respectively. In the sections that follow, we review biological impacts of non-breaking internal waves, focusing on four broad categories: (1) wave-induced concentration changes in depth-​keeping plankton, (2) wave-​induced transport of passive and depth-​keeping plankton, (3) wave-​induced environmental variability for passive plankton in a property field that varies only with depth, such as solar irradiance, and (4) wave-induced environmental variability for depth-keeping plankton and sessile organisms in a property field that is approximately constant along isopycnals, such as temperature. We then contrast time series of these properties as they apply to virtual organisms released in both linear and weakly nonlinear internal waves (Box 1).

 

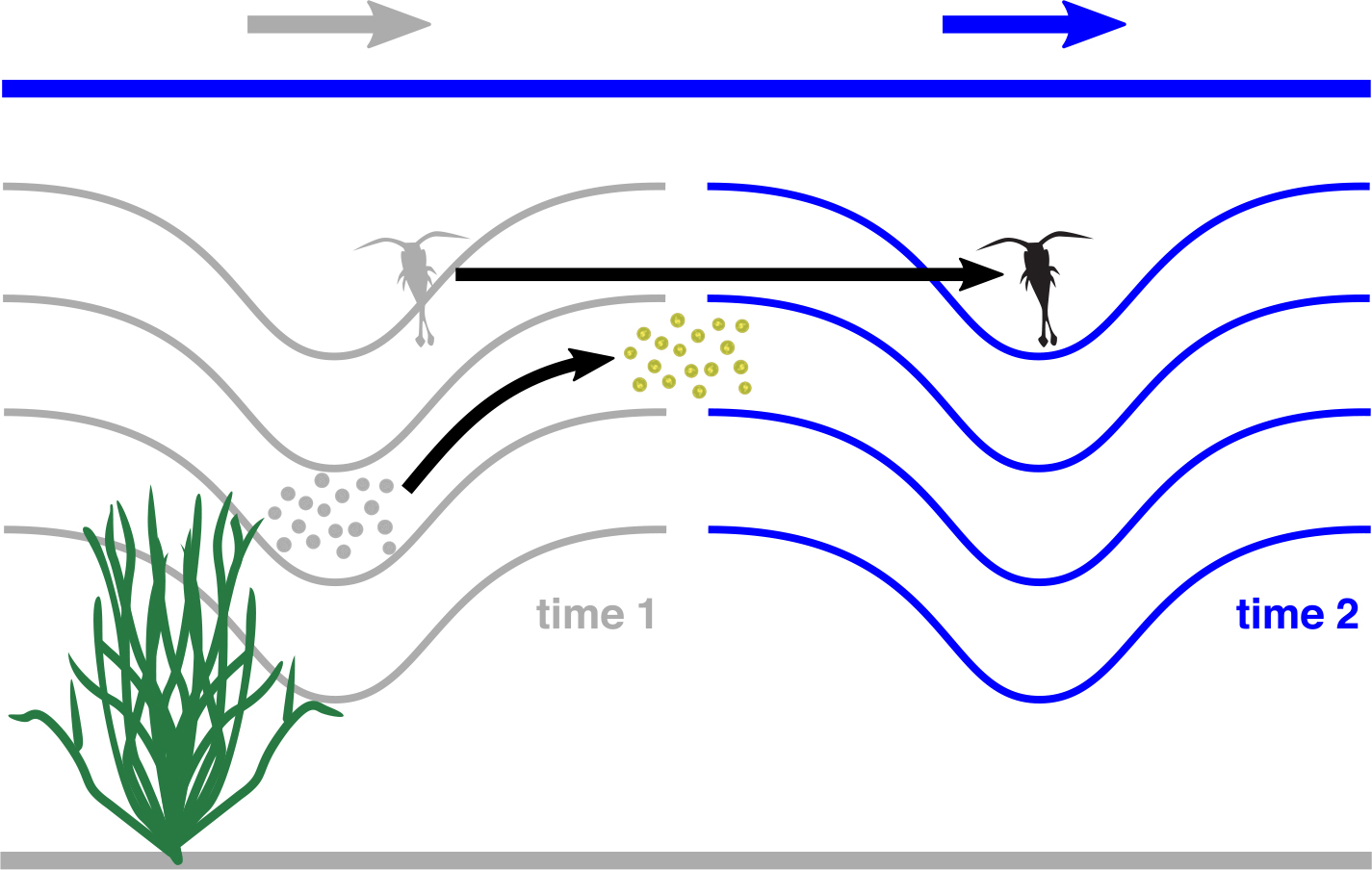
Figure 1. This article considers three categories of marine organisms: (1) passive plankton (gray and green circles), (2) depth-keeping plankton (gray and black copepods), and (3) sessile organisms (green macroalga). The gray and blue arrows show the direction of wave propagation, while the black arrows show wave-induced plankton movement between the two time steps. The first time step is in gray, except for the macroalga that is fixed. Drawings by Tracey Saxby (Chlamydomonas), Jane Hawkey (copepod), and Diana Kleine (Chlorophyta), Integration and Application Network, University of Maryland Center for Environmental Science (https://ian.umces.edu/imagelibrary/). > High res figure

 

Box 1. Internal Wave Simulations   Our heuristic examples focus on high-frequency internal waves, that is, on internal waves at the local buoyancy frequency, with periods on the order of tens of minutes. In the coastal ocean, these internal waves are ubiquitous and can take many forms, including internal tidal bores, solitary waves, wave packets, boluses, or intermediate solibores (e.g., Farmer and Smith, 1980; MacKinnon and Gregg, 2003; Bourgault et al., 2007; J. Nash et al., 2012). Here, we simulate weakly nonlinear oscillatory internal waves (Figure 2b). As internal waves steepen, they become increasingly nonlinear and induce horizontal velocities that approach the wave propagation speed (u/c → 1). Although coastal internal waves usually display some degree of nonlinearity, we also include comparisons with linear internal waves (Figure 2a). In contrast to nonlinear internal waves, linear internal waves induce weak horizontal velocities, compared to their propagation speed (u/c << 1) (Figure 2a). 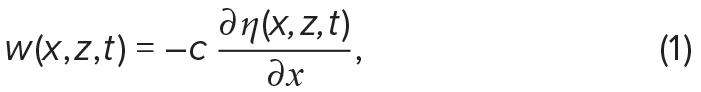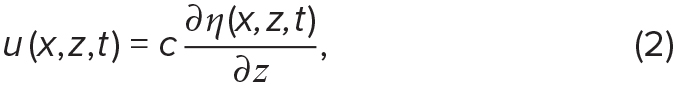Internal-wave-induced vertical and horizontal velocities, w and u, respectively, can be derived from internal wave isopycnal displacements, η (Stastna and Lamb, 2002; Chang et al., 2011): and where t is time, x is positive in the direction of wave propagation, and z is positive upwards. The shape of both linear and weakly nonlinear internal waves can be described by analytic expressions that capture the spatial distribution of η over time. 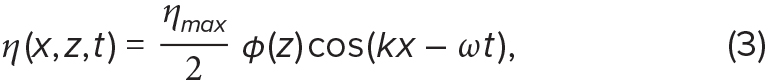For instance, the structure of a mode-1, linear progressive wave is described by a sinusoid in the horizontal (Woodson, 2018): where ηmax is the maximum isopycnal displacement, φ(z) is the wave’s vertical structure, k is the horizontal wavenumber, and ω is the wave frequency. The horizontal wavenumber and wave frequency can be calculated from the wavelength λ and the wave period T, with k = 2π/λ and ω = 2π/T. The wave propagation speed is related to the wavelength by c = λ/T. Various mathematical functions, including cnoidal functions, can be used to capture the wide range of weakly nonlinear wave shapes (see review by Apel, 2002). 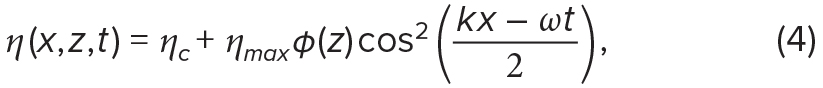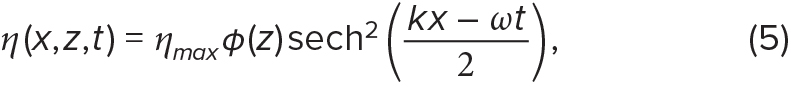The linear limit of the cnoidal function is associated with a cosine-squared wave (Equation 4), while the most nonlinear limit is associated with a hyperbolic secant wave (Equation 5), also known as a solitary wave or soliton: where ηc is the crest elevation. In solitons, isopycnals return to their equilibrium depths at infinity, thus ηc is equal to zero and not included in Equation 5. In reality, internal wave characteristics, such as wave shape and wave propagation speed, are determined by background ocean velocity and density structure. Here, for ease of comparison, we apply the same parameters to both linear and weakly nonlinear internal waves; we set ηc to 0 m, ηmax to 2.5 m, c to 0.3 m s–1, and T to 900 s (15 min). We propagate these waves in a water column of 20 m, with φ(z) = sin(–πz/H) (Figure 2). Although these wave parameters are realistic (e.g., Garwood et al., 2020), examples are provided for illustrative purposes only. To contrast the wave-induced environmental variability for sessile organisms, as well as for passive and depth-keeping plankton, we use Equation 3 to simulate linear internal waves and Equation 4 to simulate weakly nonlinear internal waves (Figure 2a,b). Passive organisms are numerically advected through these wave fields using Equations 1 and 2 evaluated at the organisms’ positions (xorg, zorg) at time t, with a time step of 1 s. Depth-keeping organisms are advected in the horizontal only using Equation 2, while sessile organisms are not moved by the flow, but the flow around them is recorded.

 

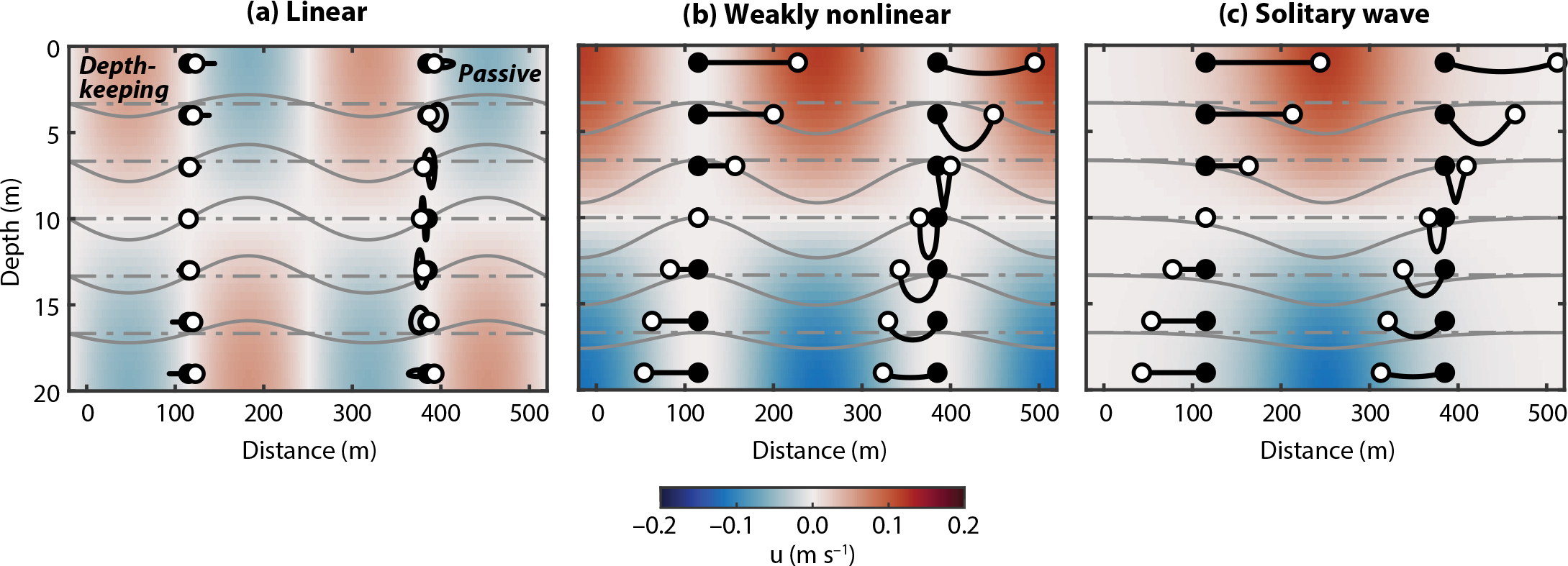
Figure 2. Paths for depth-keeping (left) and passive (right) plankton in linear (a), weakly nonlinear (b), and solitary (c) waves with parameters ηc = 0 m, ηmax = 2.5 m, c = 0.3 m s–1, T = 900 s (15 min), z = 0 to –20 m, and φ = sin(–πz/H). Black and white circles show plankton start and end points, respectively. Horizontal motions are 50% exaggerated. Colors show wave-induced horizontal velocities at the starting points of the paths, with red velocities in the direction of wave propagation. With the solitary wave, velocities are relative to the starting point of passive plankton. Gray lines show unperturbed isopycnals (dashed) and isopycnals displaced by the wave (solid). > High res figure

 

Enhanced Concentrations of Buoyant or Swimming Plankton

In propagating internal waves, the horizontal gradients of wave-induced surface horizontal velocities generate areas of convergence and divergence ahead of troughs and crests, respectively (Ewing, 1950a, 1950b). Although incompressible flows do not induce concentration changes in passive plankton, vertical swimming decouples plankton from fluid velocities and can result in accumulation (Genin et al., 2005; Hoecker-Martínez and Smyth, 2012). Internal waves, therefore, can only concentrate plankton that at least partially resist vertical velocities, such as floating eggs or vertically swimming plankton (Ewing, 1950b; Franks, 1997; Lennert-Cody and Franks, 1999, 2002; Omand et al., 2011). The areas of maximum and minimum plankton concentrations will be offset from the areas of maximum convergence and divergence and will occur above wave troughs and crests, respectively.

Buoyant surface films are also most concentrated and dispersed above internal wave troughs and crests, respectively (Ewing, 1950a,b). In low wind, the interaction of internal waves with surface films and capillary waves produces a banding pattern at the ocean’s surface: areas with concentrated surface films dampen ripples and produce surface slicks, while areas with dispersed films remain rough (Ewing, 1950a,b). These visible internal wave signatures have been exploited by biological oceanographers to assess the potential of internal waves to concentrate vertically swimming plankton: enhanced concentrations of plankton, fish larvae, and pelagic crabs have all been observed in surface slicks (Zeldis and Jillett, 1982; Shanks, 1983, 1988; Jillett and Zeldis, 1985; Shanks and Wright, 1987). Even organisms that are not vulnerable to ocean currents, such as fish and pilot whales, were observed in association with internal wave troughs (Kingsford and Choat, 1986; Moore and Lien, 2007). These relationships are likely indicative of a reactive process, in which higher trophic levels seek higher concentrations of prey and/or drift algae created by internal wave motions (Kingsford and Choat, 1986; Moore and Lien, 2007; Lévy et al., 2018). At an offshore bank, a three-way interaction between euphausiid swimming behavior, internal waves, and topography promoted near-surface shoals of euphausiids, which were then exploited by herring, seabirds, and whales (Stevick et al., 2008). Schooling fish may benefit not only from internal wave troughs concentrating vertically swimming zooplankton prey above the pycnocline but also from the waves increasing the vertical space available for schooling and feeding (Bertrand et al., 2008).

In the Benguela Current, the thickening of a turbid surface layer above internal wave troughs decreased light penetration and induced the upward vertical migration of a foraging fish (Kaartvedt et al., 2012). Thus, by affecting light penetration in the ocean, internal waves can also increase feeding opportunities for predators that must avoid their own visual predators (Kaartvedt et al., 2012). Variability in depth-​keeping abilities between planktonic prey and predators can lead to differential vertical advection by internal waves and different concentration patterns, both of which will influence trophic interactions (Macías et al., 2010; Greer et al., 2014). While they concentrate vertically swimming prey, internal waves may also concentrate floating plastic and contaminants (Shanks, 1987).

 

Horizontal Drift in Internal Waves: Stokes Drift, Eulerian Mean Flow, and Total Transport

Propagating internal waves can concentrate vertically swimming plankton locally, and these high-​concentration regions will shift in the direction of wave propagation. However, how far individual organisms will be transported will depend on wave nonlinearity: net transport will be limited in linear internal waves (Franks, 1997), whereas organisms in nonlinear internal waves may be displaced large distances (Figures 2 and 3c,f). In parts of Massachusetts Bay, for instance, patches of low chlorophyll a concentrations may be caused by nonlinear internal waves transporting phytoplankton away from the area (Lai et al., 2010). Nonlinear internal waves usually enhance onshore transport of larvae, which can promote recruitment (Shanks, 1983, 1988; Pineda, 1999; Garwood et al., 2020). However, highly energetic nonlinear internal waves can also transport larvae away from productive areas and expose them to mechanical stress, resulting in energy loss and lower survival (Ruvalcaba-Aroche et al., 2019).

In what follows, we define the Eulerian contribution to transport as the integral of horizontal currents measured at a fixed location, over a wave period. The total transport is assessed over the time period between organisms encountering two adjacent, identical wave phases (e.g., crest to crest, or trough to trough), which we define as the organisms’ residence time in the wave τ. Stokes drift results from how drifting organisms experience wave velocities and is defined as the difference between the total plankton transport and the Eulerian contribution, calculated at the organisms’ depth in an ocean at rest (Figure 3).

 

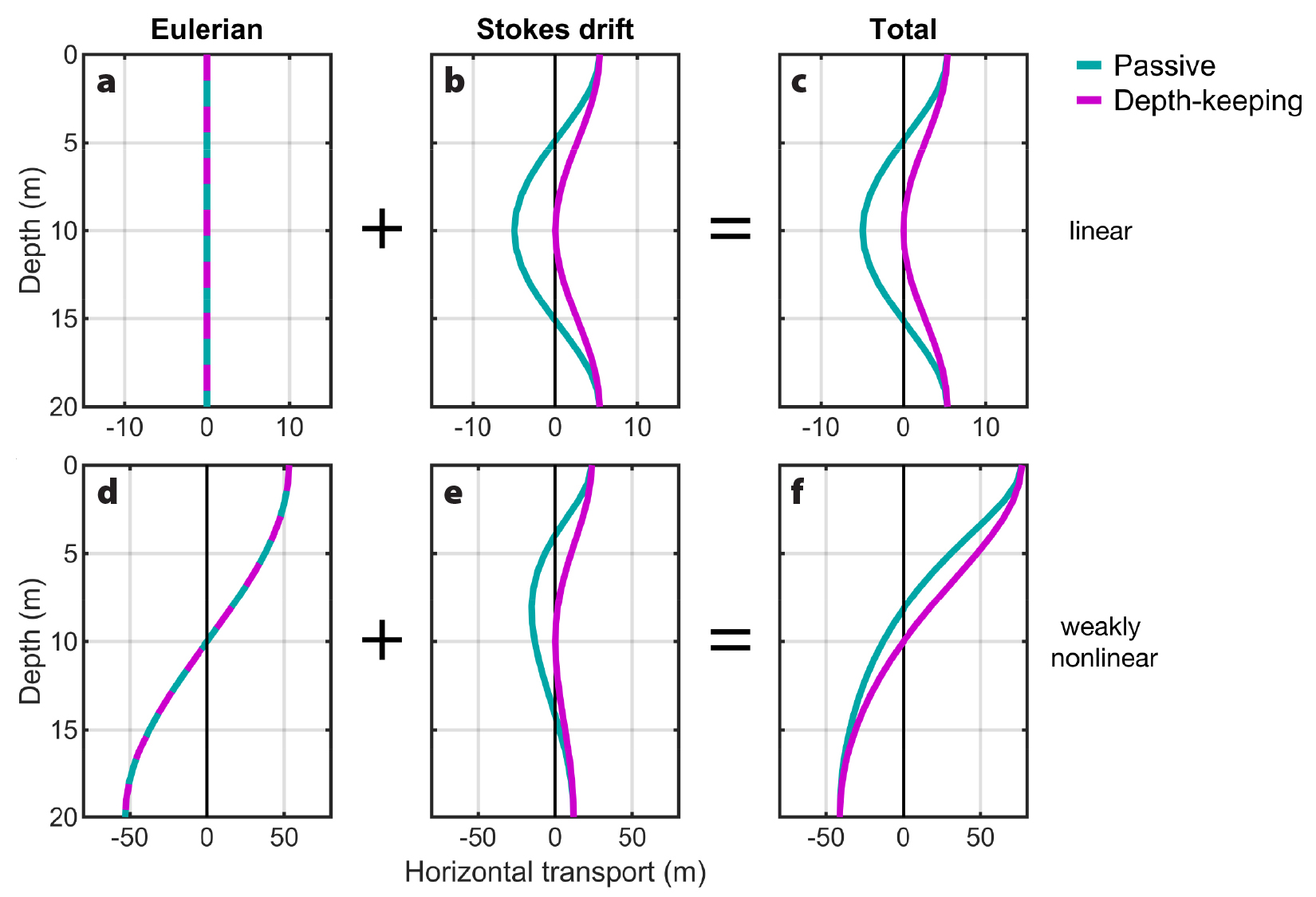
Figure 3. Wave-induced horizontal transport (m) from integrated Eulerian velocities (left) and Stokes drift (middle) for passive (teal) and depth-keeping (pink) plankton in linear (top) and weakly nonlinear (bottom) waves. Total transport is also shown (right). Note that the scale of the x-axis is different for linear and weakly nonlinear waves. > High res figure

 

Typically, only highly nonlinear internal waves are assumed to transport plankton over large distances due to the small (and often neglected) Stokes drift associated with linear internal waves (Pineda, 1994, 1999; Shanks, 1995; Lamb, 1997). Nonlinear internal waves of depression, for instance, induce wave velocities that are constantly in the direction of wave propagation above the pycnocline, driving net transport in the direction of the wave’s propagation, and vice versa at depth (Apel et al., 1985; e.g., Figure 2b,c). Thus, in nonlinear internal waves, both time-mean Eulerian velocities and Stokes drift contribute to transport. Linear internal waves, however, induce alternating positive and negative wave velocities of equal magnitudes at all depths (e.g., Figure 2a). The Eulerian transport is therefore zero; net transport for drifting organisms is due only to Stokes drift (Thorpe, 1968; Dewar, 1980; Franks et al., 2020). Although Stokes drift is non-zero in both linear and nonlinear internal waves, it is stronger in nonlinear internal waves (Figures 2 and 3b,e).

For internal waves in the absence of a mean flow, Stokes drift is in the direction of wave propagation for both passive and depth-keeping organisms near the top and bottom of the water column (Henderson, 2016; Franks et al., 2020; Figures 2a and 3b,e). Mid-water, passive organisms are transported in the opposite direction, while there is no net transport for depth-keeping organisms (Franks et al., 2020; Figures 2a and 3b,e). In all cases, wave-induced horizontal transport will occur along the same axis as internal wave propagation (Lamb, 1997), and while this may be in the cross-shore direction for many coastal internal waves (e.g., Lee, 1961; Shroyer et al., 2011; Richards et al., 2013; Colosi et al., 2018; Sinnett et al., 2018), some coastlines favor along-shore displacements (Liévana MacTavish et al., 2016). At other sites, the direction of internal wave propagation can vary spatially as wave trains refract through background currents and over sloping bathymetry (Thomas et al., 2016; Hamann et al., 2018). Moreover, interactions between internal waves and depth-varying background currents can modify both the magnitude and the direction of these predicted wave-induced transports (Garwood et al., 2020).

The specific paths of plankton in internal waves will dictate the environment they are exposed to (Box 2). Depth-​keeping and passive plankton spend more time in parts of internal waves where currents are moving in the same direction as propagation, (e.g., above wave troughs and below wave crests in linear waves; Figure 2), and less time in parts of the waves where currents are in the opposite direction to wave propagation. In our linear internal wave example, for instance, notice how both passive and depth-​keeping plankton spend more time being moved in the positive direction than in the negative direction (Figure 4b,c). Our weakly nonlinear wave example makes this particularly obvious. Notice how the residence time in the wave τ (Box 2)—shown by the length of the planktonic records—decreases with depth: planktonic records in the top half of the water column (warm colors, positive displacements) extend past the wave period (dashed line), while planktonic records in the bottom half (cold colors, negative displacements) end before the wave period. Residence time also varies in the linear wave although differences are small and thus less noticeable (Figure 4b,c).

 

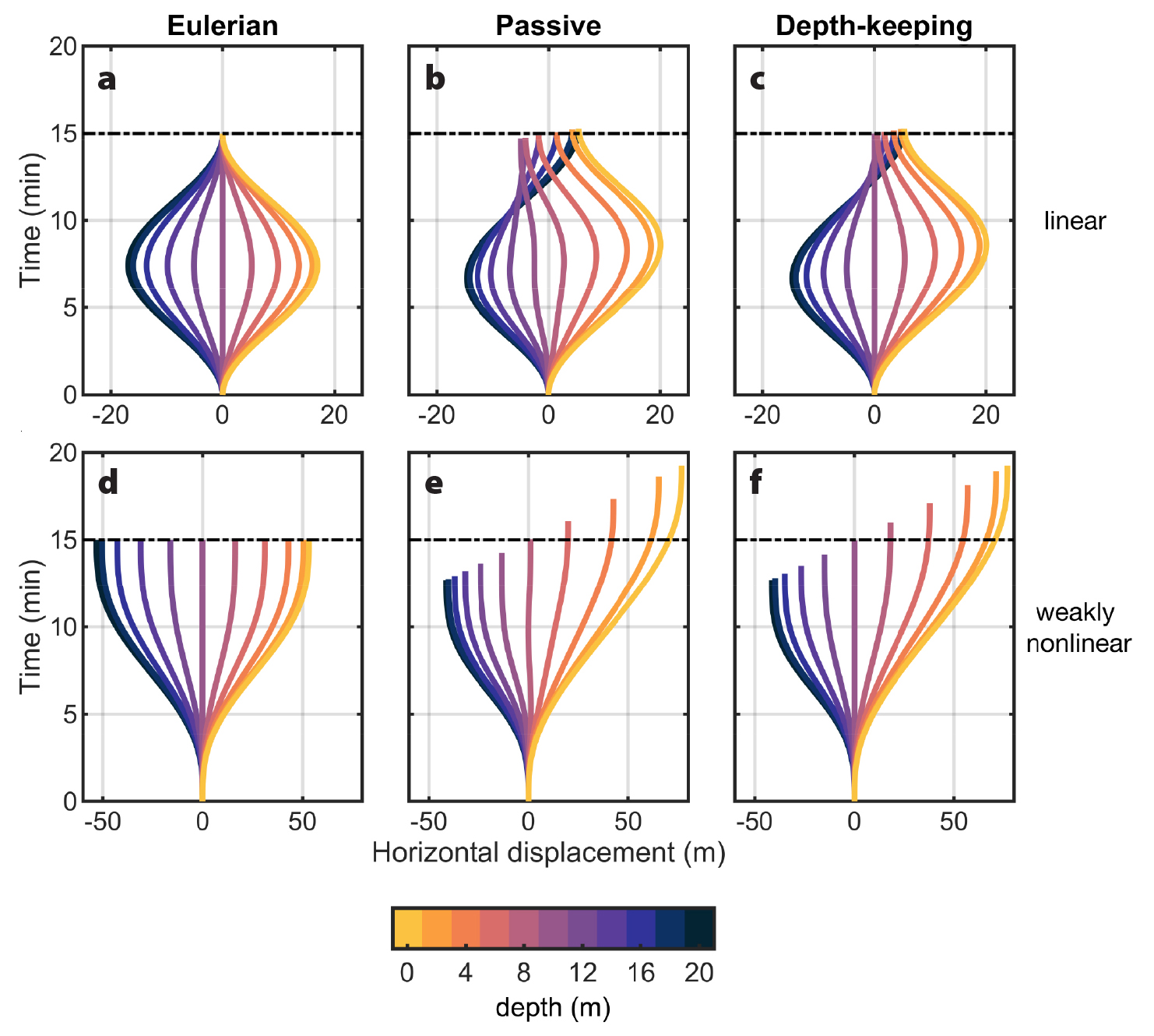
Figure 4. Time series of horizontal displacements (m) for passive (middle) and depth-keeping (right) plankton in linear (top) and nonlinear (bottom) internal waves. Horizontal displacements calculated by integrating Eulerian velocities (left) are also shown. Colors indicate organisms’ depths, while horizontal dashed lines show the wave periods (15 min). Note that the scale of the x-axis is different for linear and weakly nonlinear waves. > High res figure

 

Box 2. Environmental Conditions Encountered by Virtual Marine Organisms   We use solar irradiance, normalized by surface solar irradiance, QI = Iz/I0, as an example of an environmental property that depends only on depth, and temperature, QT, as an example of an ocean property that is associated with ocean density (Figure 5). 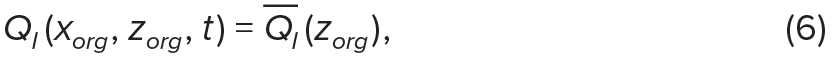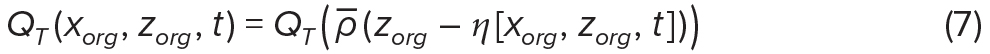The environmental conditions for each virtual organism were calculated from its horizontal and vertical position at every time step, with and where QI— and ρ— are the vertical profiles of normalized solar irradiance and density, respectively, in an unperturbed ocean (Figure 5a). Thus, QT(ρ—) represents the temperature profile in an unperturbed ocean (Figure 5d), and Equation 7 accounts for how it is modified by the wave (Figure 5e). Note that although organisms may be moved vertically by internal waves, which will affect their total solar irradiance, the vertical profile of solar irradiance itself is not modified by the waves (Figure 5b). Integrating Environmental Conditions Generally, the time-integrated environmental conditions encountered by marine organisms (represented by bold variables) can be described by for an environmental property that varies with depth (Qz) and by for an environmental property that is constant along isopycnals (Qρ) and deformed by internal waves. Importantly, these integrations must be performed while following planktonic organisms. The period over which these integrations are performed, τ, denotes the residence time of the organisms in the wave. We defined this to be the time between an organism encountering two adjacent, identical wave phases (e.g., crest to crest, or trough to trough). Only in the case of sessile organisms will τ always be equal to the intrinsic wave period. Depth-keeping plankton and sessile organisms remain at fixed depths throughout the passage of an internal wave. Therefore, their overall exposure to an environmental property that depends only on depth remains unaffected by internal waves. In such cases, Equation 8 can be simplified to Qz = τ Qz(z0), where z0 is the organisms’ depth before and throughout the wave. Similarly, for Qρ constant in time, passive organisms that remain on an isopycnal have Qρ = τ Qρ(ρ0), where ρ0 is the water density surrounding the passive organisms before and throughout the wave. The discussion here focuses on cases in which internal waves influence marine organisms’ time-integrated environmental conditions, such as irradiance for passive plankton moved vertically, and temperature for depth-keeping and sessile organisms.

 

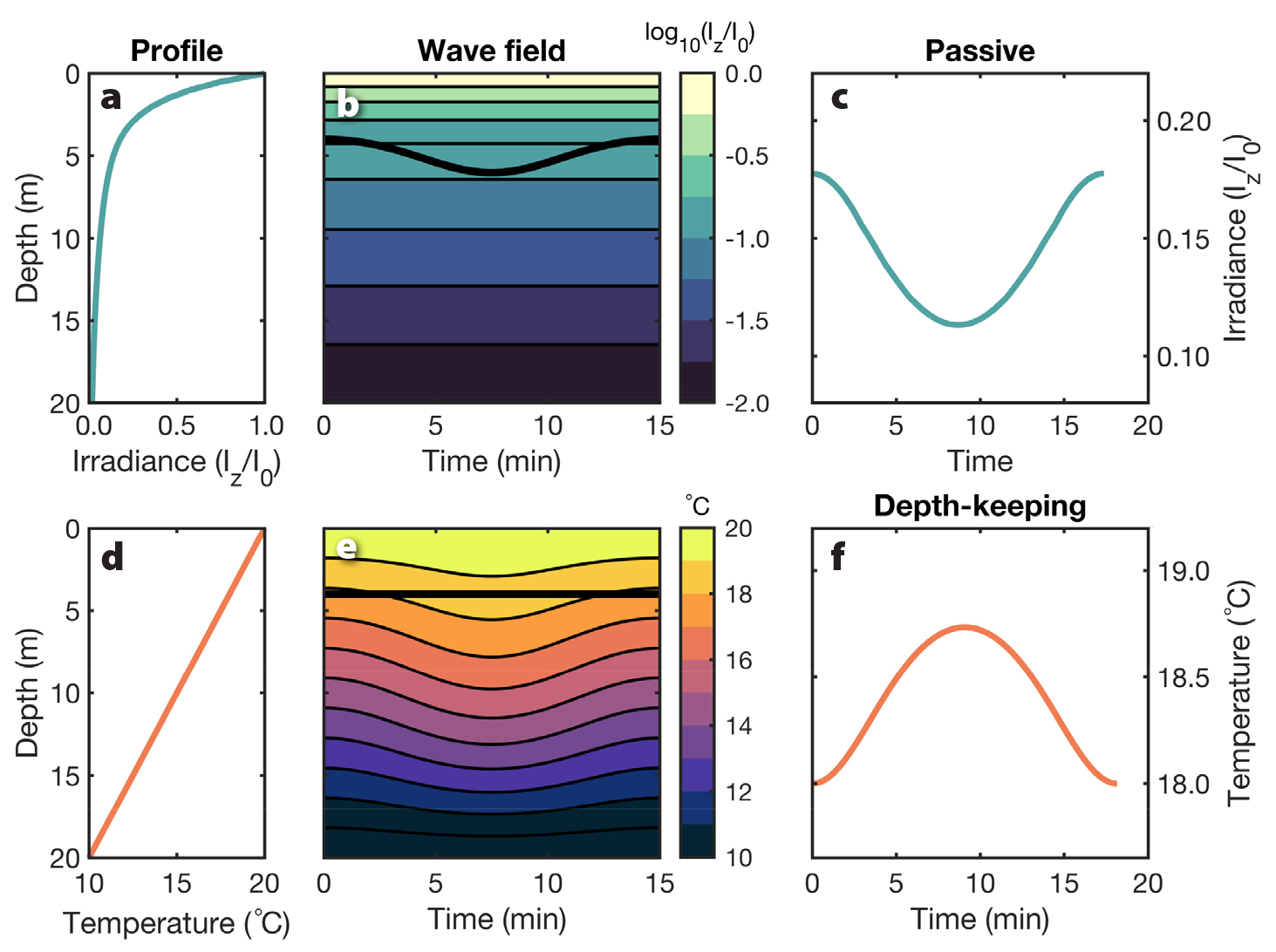
Figure 5. Irradiance (a) and temperature (d) profiles in an unperturbed ocean, with associated wave fields (b and e) for the weakly nonlinear internal waves illustrated in Figure 2. Time series of irradiance (c) and temperature (f) experienced by passive and depth-keeping plankton, respectively, at the depth shown by the thick black lines in wave fields (b) and (e). > High res figure

 

Passive Plankton in Vertical Gradients Unaffected by Internal Waves

In the ocean, a few environmental properties such as solar irradiance and pressure are determined predominantly by depth. Because irradiance is “stationary” in the water column, wave-induced vertical displacements will move passive phytoplankton through irradiance gradients (Figure 5), potentially changing their growth rates (e.g., Kamykowski, 1974; Kahru, 1983; Holloway and Denman, 1989; Evans et al., 2008). Bands of enhanced chlorophyll a have been observed via remote sensing and by drifting profilers, consistent with a deep chlorophyll maximum being lifted by internal waves (da Silva, 2002; Muacho et al., 2013; Lucas et al., 2016). This process can increase primary productivity compared to production in an unperturbed ocean (da Silva, 2002; Muacho et al., 2013; but see also Holloway and Denman, 1989). In the South China Sea, regions in which internal waves were present but not breaking were associated with higher chlorophyll a than nearby regions without much internal wave activity (Pan et al., 2012).

To properly assess how vertical motions affect primary production, however, the phasing of internal waves with respect to variable surface irradiance must be taken into account. For instance, the phasing of M2 internal tides with respect to daylight hours and the phasing of higher-​frequency waves with respect to patchy cloud coverage both have the potential to modulate primary production (Kamykowski, 1974; Evans et al., 2008; Muacho et al., 2013). High-frequency internal waves may affect primary production more strongly than internal tides, as phytoplankton displayed higher daily photosynthesis when subjected to rapidly changing light than phytoplankton subjected to slowly fluctuating light, despite an overall equal average light level (Flameling and Kromkamp, 1997). Strongly nonlinear internal wave packets can induce downward isopycnal displacements of tens of meters; their passage can therefore significantly deepen any isopycnal-​following subsurface chlorophyll maximum and reduce the total solar irradiance that reaches photosynthetic organisms (Haury et al., 1983). However, internal motions need not be that large to influence plankton (Cheriton et al., 2009). Bottle experiments in Toolik Lake, Alaska, demonstrated that internal waves with small amplitudes (~1 m) and periods of 2–6 h could modify photosynthesis by –15% to 200%, compared to an unperturbed water column (Evans et al., 2008).

Linear internal waves move passive organisms up and down an equal vertical distance from their equilibrium depths in an unperturbed ocean (Figure 2a). Passive phytoplankton, therefore, are subjected to both enhanced and decreased solar irradiance throughout a wave compared to their exposure in an unperturbed ocean (Figure 6). However, because of the exponential decrease of irradiance with depth (Figure 5a), the enhancement associated with upward motions will be greater than the depletion associated with downward motions. In weakly nonlinear internal waves of depression, isopycnals are only displaced downward (Figure 2b,c), so passive phytoplankton are only exposed to decreased solar irradiance (Figure 6). Using a Type III irradiance profile (Paulson and Simpson, 1977; Figure 5a), we show that accounting for Stokes drift in both linear and nonlinear waves reduces estimates of the averaged solar irradiance received by phytoplankton in the top half of the water column due to longer residence time at the trough of the waves, and vice versa at depth (Figure 6c,f). For environmental properties that increase with depth, such as pressure, passive organisms would be subjected to enhancements in a weakly nonlinear internal wave of depression.

 

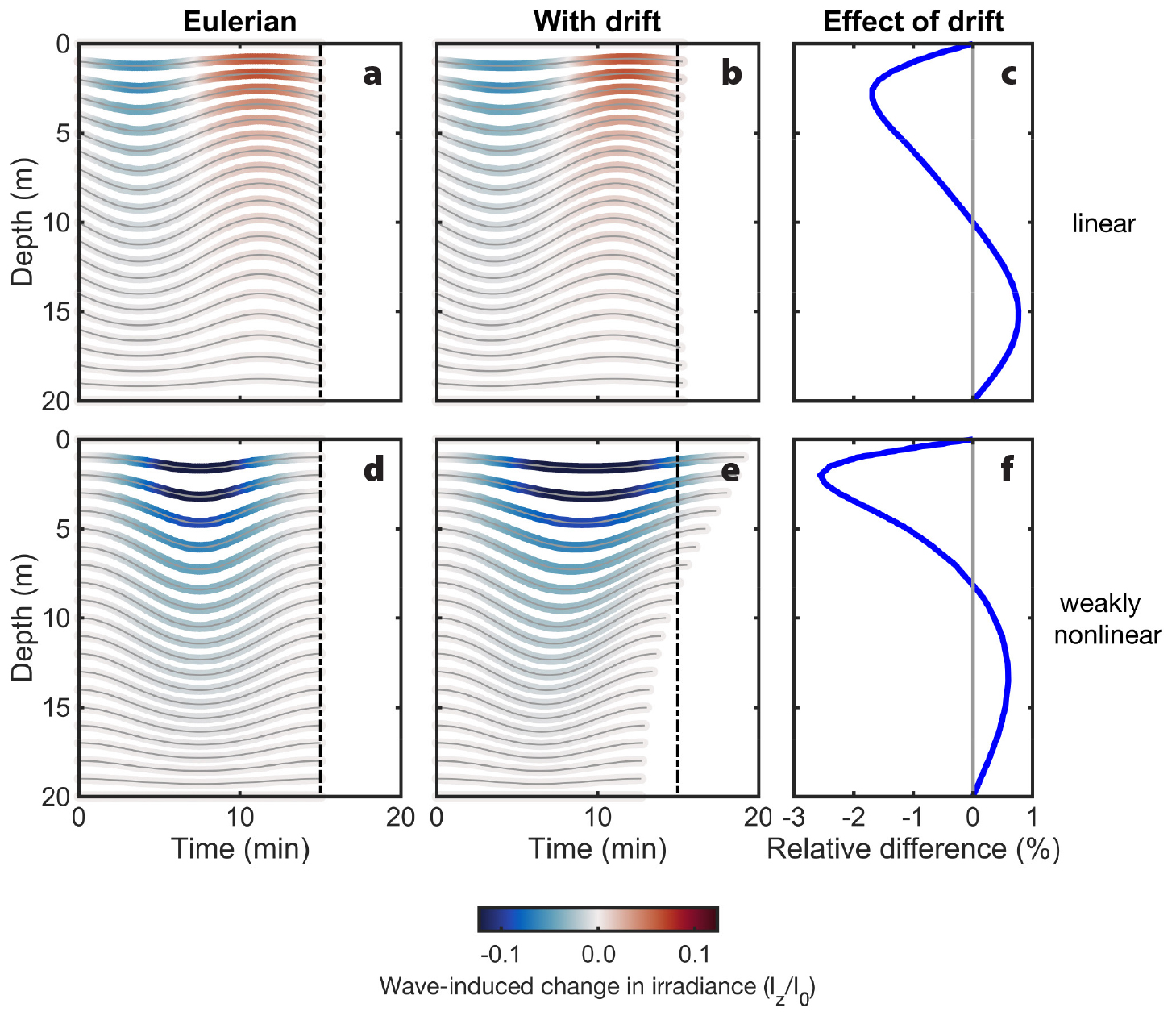
Figure 6. Wave-induced change in irradiance, normalized to surface irradiance (Iz/I0), estimated for passive organisms using isopycnal displacements at a point (Eulerian, at left) and including drift (middle) in the linear (top) and nonlinear (bottom) internal waves. The relative effect of drift on the organisms’ average irradiance exposure (%) is also shown (right). At depth, including drift increases the average irradiance estimated (positive differences) because it reduces the time organisms spend at the trough of the wave. > High res figure

 

Because pressure increases with depth, plankton that regulate their buoyancy through gas vacuoles, such as cyanobacteria (Oliver, 1994), will become less buoyant if internal waves displace them to greater depth, and vice versa. As any diver knows, the effects of these displacements require control because they are magnified by the positive feedback between depth and gas compression. Thus, internal waves could increase the metabolic costs of depth regulators that rely on gas vacuoles or swim bladders. In laboratory experiments, gray mullet fish larvae exhibited higher survival when water motions kept them below the water surface, thus preventing excessive bladder inflation (C.E. Nash et al., 1977). Moreover, early sunlight exposure can be fatal to these larvae (C.E. Nash et al., 1974), and seabirds have been observed to feed where internal waves bring organisms closer to the surface (Haney, 1987); it is possible that fluctuations in the internal wave regime thus modulate the survival of mullet fish larvae and other zooplankton.

 

Organisms at a Fixed Depth in Vertical Gradients Displaced by Internal Waves

In the absence of mixing and over short timescales, many ocean properties such as temperature, nutrient levels, oxygen, or phytoplankton concentrations are often relatively constant along isopycnals. This means that isopycnal-following phytoplankton communities that are moved up and down by internal waves are exposed to fluctuating irradiance, but remain surrounded by water at a constant temperature, for example. However, organisms that move with respect to water parcels, including those that maintain a fixed depth, cross isopycnals as internal waves propagate past them (Figure 5e,f; Garwood et al., 2020). Grazers that can resist internal-wave-induced vertical displacements may therefore see layers of high phytoplankton density advected to them from above or below (Witman et al., 1993). Many studies have also documented internal waves displacing deep waters to shallower depths in kelp forests (Zimmerman and Kremer, 1984; McPhee-Shaw et al., 2007), macroalgal communities (Ladah et al., 2012), and coral reefs (Leichter et al., 1996, 2006). Because these deeper waters can host higher zooplankton concentrations, internal waves may bring “plankton storms” that supply reefs with both larvae and food (Leichter et al., 1998). The cooler, nutrient-rich waters moved by the internal waves may also deliver nutrients (Zimmerman and Kremer, 1984; Leichter et al., 1996, 2003) and decrease thermal stress (Wall et al., 2015; Reid et al., 2019), likely influencing zonation in coastal benthic environments. Although the water motions eventually reverse, internal waves can have a lasting impact if mixing occurs or if biological processes such as prey capture and nutrient absorption occur more rapidly than the timescale of each wave.

In Monterey Bay, California, high-​frequency internal waves cause intrusions of low oxygen, low pH waters in coastal ecosystems (Booth et al., 2012; Walter et al., 2014). In these shallow water environments, market squid lay their egg capsules directly on the seafloor (Zeidberg et al., 2012); by modulating oxygen, pH, and temperature, internal waves may thus affect squid embryonic development (Navarro et al., 2016). Not only will wave-induced low oxygen, low pH intrusions modify environmental conditions for sessile organisms or egg capsules, they can also determine the vertical distribution of zooplankton (Wishner et al., 2013). The effects of internal waves on water properties, however, need not be instantaneous. At Dongsha Atoll in the South China Sea, for example, lasting depletion in dissolved oxygen was observed, potentially caused by internal waves delivering enhanced particulate organic matter that was subsequently degraded by microbes (Wang et al., 2007).

Similar to sessile organisms, depth-​keeping plankton encounter a range of along-​isopycnal properties throughout internal waves. However, unlike sessile organisms, depth-​keeping plankton drift with internal waves (Shanks, 1983; Shanks and Wright, 1987; Pineda, 1999; Franks et al., 2020); thus, average environmental conditions differ for sessile organisms and depth-keeping plankton, even at the same depth (Figure 7).

Where temperature gradients exist, linear internal waves that propagate past sessile and depth-keeping organisms induce both warm and cold water temperature anomalies, shown by the positive (red) and negative (blue) temperature changes in Figure 7a,b. In weakly nonlinear internal waves of depression, however, the same organisms only encounter warm temperature anomalies as warmer waters are displaced downward (provided temperature decreases with depth; Figure 7d,e, where all lines are red). In both linear and weakly nonlinear waves propagating through a linear temperature gradient (Figure 5d), the average water temperature depth-​keeping plankton experience over a single wave is higher in the top half of the water column than the average temperature of water passing over sessile organisms, and vice versa at depth (Figure 7c,f). This difference is due to the fact that planktonic organisms above mid-water spend more time drifting with wave troughs (where temperatures are warmer) than sessile organisms spend in the same troughs, and vice versa at depth (Figure 7—notice the relative lengths of red areas). In general, the trends described will hold for any fluid property that decreases with depth. However, the magnitude of the “drifting effect” and its vertical structure will be set by the vertical gradient of fluid properties. For other environmental properties, such as nutrient levels that often increase with depth, the passage of internal waves of depression will result in depletions for fixed-depth organisms.

 

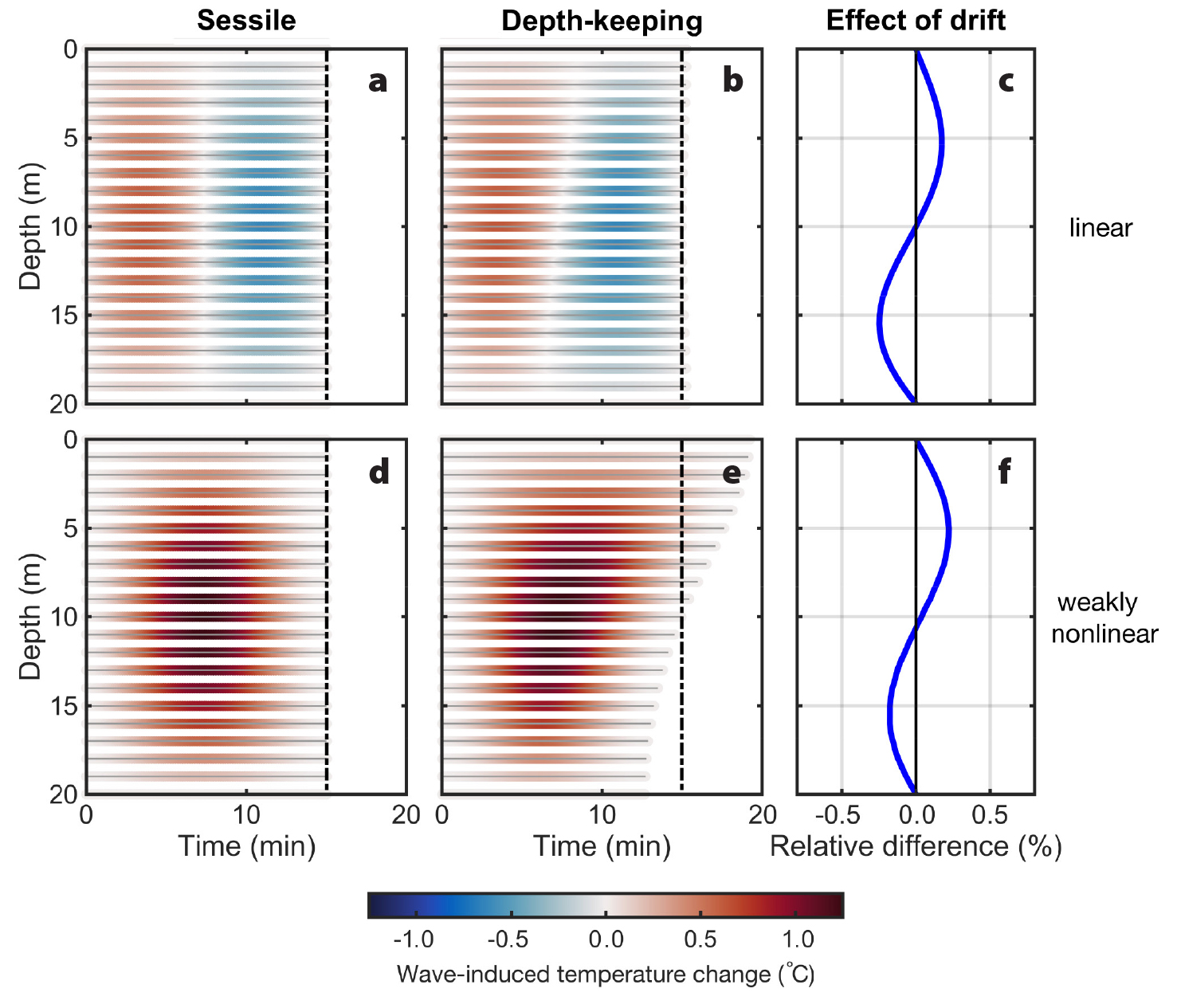
Figure 7. Wave-induced temperature change (°C) experienced by sessile (left) and depth-​keeping (middle) organisms in the linear (top) and weakly nonlinear (bottom) internal waves. The relative difference in the average temperature experienced by depth-keeping plankton compared to sessile organisms (%) is also shown (right). Positive differences indicate higher temperatures for depth-keeping plankton. > High res figure

 

Conclusions

Internal waves modulate the immediate environments of marine organisms either by displacing the organisms vertically or by advecting waters with different properties to their depths. In our heuristic weakly nonlinear internal wave example, passive plankton at 5 m were displaced a maximum of 2.3 m downward, which reduced their total irradiance exposure by 18.7% over a period of 16.7 minutes. In the same waves, depth-keeping plankton at the same initial depth were exposed to an average wave-induced temperature increase of 0.5°C (or 2.7%) over 17.6 minutes. Compared to the 15-minute wave period, Stokes drift in the direction of wave propagation increased the residence time of both passive and depth-keeping plankton at 5 m by 11% and 17%, respectively, further enhancing internal wave effects. Even when both irradiance and temperature decrease with depth, weakly nonlinear internal waves of depression decrease the irradiance exposure of passive plankton, while the same waves instead increase the temperatures experienced by organisms at a fixed depth (Figures 6 and 7). These opposing trends are explained by the fact that whenever internal waves move passive organisms to greater depths (where irradiance is reduced), they displace warmer waters from shallower depths to fixed-depth organisms. By resisting vertical velocities, fixed-depth organisms essentially move in the direction opposite to passive organism displacements, relative to the wave field. Overall, mooring observations of wave-perturbed oceans provide a good characterization of the environment of sessile organisms. However, to truly capture the internal-wave-induced environmental variability for plankton, horizontal drift should also be considered. For example, for passive and depth-​keeping plankton initially located at 5 m, total horizontal transport in our weakly nonlinear internal waves was, respectively, ~30 m and ~50 m in the direction of wave propagation. Although our examples focused on the simple case of an internal wave without ambient flow, the effects demonstrated would be magnified in the presence of large ambient velocities.

 

Acknowledgments

We thank Peter Franks, Jesse Cusack, Martín Hoecker-Martinez, C. Brock Woodson, and a third anonymous reviewer for their helpful comments. We are also grateful to Eddie Kisfaludy at SciFly for generously providing the aerial photograph. The material is based upon work supported by the National Science Foundation under Grant No. OCE-1459393. JCG was partially funded by an NSERC doctoral fellowship.

Garwood, J.C., R.C. Musgrave, and A.J. Lucas. 2020. Life in internal waves. Oceanography 33(3):38–49, https://doi.org/10.5670/oceanog.2020.313.

Apel, J.R., J.R. Holbrook, A.K. Liu, and J.J. Tsai. 1985. The Sulu Sea internal soliton experiment. Journal of Physical Oceanography 15(12):1,625–1,651, https://doi.org/10.1175/1520-0485(1985)015​<1625:TSSISE>2.0.CO;2.

Apel, J.R. 2002. Oceanic internal waves and solitons. Pp. 1–40 in An Atlas of Internal Solitary-like Waves and Their Properties. C.R. Jackson and J.R. Apel, eds, Global Ocean Associates.

Bertrand, A., F. Gerlotto, S. Bertrand, M. Gutiérrez, L. Alza, A. Chipollini, E. Díaz, P. Espinoza, J. Ledesma, R. Quesquén, and others. 2008. Schooling behaviour and environmental forcing in relation to anchoveta distribution: An analysis across multiple spatial scales. Progress in Oceanography 79(2–4):264–277, https://doi.org/​10.1016/j.pocean.2008.10.018.

Booth, J.A.T., E.E. McPhee-Shaw, P. Chua, E. Kingsley, M. Denny, R. Phillips, S.J. Bograd, L.D. Zeidberg, and W.F. Gilly. 2012. Natural intrusions of hypoxic, low pH water into nearshore marine environments on the California coast. Continental Shelf Research 45:108–115, https://doi.org/10.1016/​j.csr.2012.06.009.

Bourgault, D., M.D. Blokhina, R. Mirshak, and D.E. Kelley. 2007. Evolution of a shoaling internal solitary wavetrain. Geophysical Research Letters 34(3):1–5, https://doi.org/​10.1029/​2006GL028462.

Chang, M.-H., R.-C. Lien, Y.-J. Yang, and T.-Y. Tang. 2011. Nonlinear internal wave properties estimated with moored ADCP measurements. Journal of Atmospheric and Oceanic Technology 28:802–815, https://doi.org/10.1175/2010JTECHO814.1.

Cheriton, O.M., M.A. McManus, M.T. Stacey, and J.V. Steinbuck. 2009. Physical and biological controls on the maintenance and dissipation of a thin phytoplankton layer. Marine Ecology Progress Series 378(2003):55–69, https://doi.org/10.3354/meps07847.

Colosi, J.A., N. Kumar, S.H. Suanda, T.M. Freismuth, and J.H. MacMahan. 2018. Statistics of internal tide bores and internal solitary waves observed on the inner continental shelf off Point Sal, California. Journal of Physical Oceanography 48(1):123–143, https://doi.org/10.1175/JPO-D-17-0045.1.

da Silva, J.C.B. 2002. On the observability of internal tidal waves in remotely-sensed ocean colour data. Geophysical Research Letters 29(12):1569, https://doi.org/10.1029/2001GL013888.

Dewar, W.K. 1980. The Effect of Internal Waves on Neutrally Buoyant Floats and Other Near-Lagrangian Tracers. Master’s Thesis, Massachusetts Institute of Technology, 78 pp.

Evans, M.A., S. MacIntyre, and G.W. Kling. 2008. Internal wave effects on photosynthesis: Experiments, theory, and modeling. Limnology and Oceanography 53(1):339–353, https://doi.org/​10.4319/​lo.2008.53.1.0339.

Ewing, G.C. 1950a. Relation between band slicks at the surface and internal waves in the sea. Science 111(2874):91–94, https://doi.org/10.1126/science.111.2874.91-a.

Ewing, G.C. 1950b. Slicks, surface films and internal waves. Journal of Marine Research 9(3):161–187.

Farmer, D.M., and J.D. Smith. 1980. Tidal interaction of stratified flow with a sill in Knight Inlet. Deep Sea Research Part A 27(3–4):239–246, https://doi.org/​10.1016/​0198-0149(80)90015-1.

Flameling, I.A., and J. Kromkamp. 1997. Photoacclimation of Scenedesmus protuberans (Chlorophyceae) to fluctuating irradiances simulating vertical mixing. Journal of Plankton Research 19(8):1,011–1024, https://doi.org/10.1093/plankt/19.8.1011.

Franks, P.J.S. 1997. Spatial patterns in dense algal blooms. Limnology and Oceanography 42(5, part 2):1,297–1,305, https://doi.org/10.4319/lo.1997.42.5_part_2.1297.

Franks, P.J.S., J.C. Garwood, M. Ouimet, J. Cortes, R.C. Musgrave, and A.J. Lucas. 2020. Stokes drift of plankton in linear internal waves: Cross-shore transport of neutrally buoyant and depth-​keeping organisms. Limnology and Oceanography 65(6):1,286–1,296, https://doi.org/10.1002/lno.11389.

Garwood, J.C., A.J. Lucas, P. Naughton, M.H. Alford, P.L.D. Roberts, J.S. Jaffe, L. DeGelleke, and P.J.S. Franks. 2020. A novel cross-shore transport mechanism revealed by subsurface, robotic larval mimics: Internal wave deformation of the background velocity field. Limnology and Oceanography 65(7):1,456–1,470, https://doi.org/​10.1002/lno.11400.

Genin, A., J.S. Jaffe, R. Reef, C. Richter, and P.J.S. Franks. 2005. Swimming against the flow: A mechanism of zooplankton aggregation. Science 308(5723):860–862, https://doi.org/​10.1126/​science.1107834.

Greer, A.T., R.K. Cowen, C.M. Guigand, J.A. Hare, and D. Tang. 2014. The role of internal waves in larval fish interactions with potential predators and prey. Progress in Oceanography 127:47–61, https://doi.org/​10.1016/j.pocean.2014.05.010.

Hamann, M.M., M.H. Alford, and J.B. Mickett. 2018. Generation and propagation of nonlinear internal waves in sheared currents over the Washington continental shelf. Journal of Geophysical Research 123(4):2,381–2,400, https://doi.org/​10.1002/2017JC013388.

Haney, C.J. 1987. Ocean internal waves as sources of small-scale patchiness in seabird distribution on the Blake Plateau. The Auk 104(1):129–133, https://doi.org/10.2307/4087244.

Haury, L.R., P.H. Wiebe, M.H. Orr, and M.G. Briscoe. 1983. Tidally generated high-frequency internal wave packets and their effects on plankton in Massachusetts Bay. Journal of Marine Research 41(1):65–112, https://doi.org/​10.1357/​002224083788223036.

Henderson, S.M. 2016. Upslope internal-wave Stokes drift, and compensating downslope Eulerian mean currents, observed above a lakebed. Journal of Physical Oceanography 46(6):1,947–1,961, https://doi.org/​10.1175/JPO-D-15-0114.1.

Hoecker-Martínez, M.S., and W.D. Smyth. 2012. Trapping of gyrotactic organisms in an unstable shear layer. Continental Shelf Research 36:8–18, https://doi.org/10.1016/j.csr.2012.01.003.

Holloway, G., and K. Denman. 1989. Influence of internal waves on primary production. Journal of Plankton Research 11(2):409–414, https://doi.org/​10.1093/plankt/11.2.409.

Inall, M.E., G.I. Shapiro, and T.J. Sherwin. 2001. Mass transport by non-linear internal waves on the Malin Shelf. Continental Shelf Research 21(13–14):1,449–1,472, https://doi.org/​10.1016/S0278-4343(01)00020-6.

Jillett, J.B., and J.R. Zeldis. 1985. Aerial observations of surface patchiness of a planktonic crustacean. Bulletin of Marine Science 37(2):609–619.

Kaartvedt, S., T.A. Klevjer, and D.L. Aksnes. 2012. Internal wave-mediated shading causes frequent vertical migrations in fishes. Marine Ecology Progress Series 452:1–10, https://doi.org/10.3354/meps09688.

Kahru, M. 1983. Phytoplankton patchiness generated by long internal waves: A model. Marine Ecology Progress Series 10:111–117, https://doi.org/10.3354/meps010111.

Kamykowski, D. 1974. Possible interactions between phytoplankton and semidiurnal internal tides. Journal of Marine Research 32(1):67–89.

Kingsford, M.J., and J.H. Choat. 1986. Influence of surface slicks on the distribution and onshore movement of small fish. Marine Biology 91:161–171, https://doi.org/10.1007/BF00569432.

Ladah, L.B., A. Filonov, M.F. Lavín, J.J. Leichter, J.A. Zertuche-González, and D.M. Pérez-Mayorga. 2012. Cross-shelf transport of sub-thermocline nitrate by the internal tide and rapid (3-6 h) incorporation by an inshore macroalga. Continental Shelf Research 42:10–19, https://doi.org/10.1016/​j.csr.2012.03.010.

Lai, Z., C. Chen, R.C. Beardsley, B. Rothschild, and R. Tian. 2010. Impact of high-​frequency nonlinear internal waves on plankton dynamics in Massachusetts Bay. Journal of Marine Research 68(2):259–281, https://doi.org/​10.1357/002224010793721415.

Lamb, K.G. 1997. Particle transport by nonbreaking, solitary internal waves. Journal of Geophysical Research 102(C8):18641, https://doi.org/​10.1029/​97JC00441.

Lee, O.S. 1961. Observations on internal waves in shallow water. Limnology and Oceanography 6(3):312–321, https://doi.org/​10.4319/lo.1961.6.3.0312.

Leichter, J.J., S.R. Wing, S.L. Miller, and M.W. Denny. 1996. Pulsed delivery of subthermocline water to Conch Reef (Florida Keys) by internal tidal bores. Limnology and Oceanography 41(7):1,490–1,501, https://doi.org/10.4319/lo.1996.41.7.1490.

Leichter, J.J., G. Shellenbarger, S.J. Genovese, and S.R. Wing. 1998. Breaking internal waves on a Florida (USA) coral reef: A plankton pump at work? Marine Ecology Progress Series 166:83–97, https://doi.org/10.3354/meps166083.

Leichter, J.J., H.L. Stewart, and S.L. Miller. 2003. Episodic nutrient transport to Florida coral reefs. Limnology and Oceanography 48(4):1,394–1,407, https://doi.org/10.4319/lo.2003.48.4.1394.

Leichter, J.J., B. Helmuth, and A.M. Fischer. 2006. Variation beneath the surface: Quantifying complex thermal environments on coral reefs in the Caribbean, Bahamas and Florida. Journal of Marine Research 64(4):563–588, https://doi.org/​10.1357/​002224006778715711.

Lennert-Cody, C.E., and P.J.S. Franks. 1999. Plankton patchiness in high-frequency internal waves. Marine Ecology Progress Series 186:59–66, https://doi.org/10.3354/meps186059.

Lennert-Cody, C.E., and P.J.S. Franks. 2002. Fluorescence patches in high-frequency internal waves. Marine Ecology Progress Series 235:29–42, https://doi.org/10.3354/meps235029.

Lévy, M., P.J.S. Franks, and K.S. Smith. 2018. The role of submesoscale currents in structuring marine ecosystems. Nature Communications 9(1):4758, https://doi.org/10.1038/s41467-018-07059-3.

Liévana MacTavish, A., L.B. Ladah, M.F. Lavín, A. Filonov, F.J. Tapia, and J. Leichter. 2016. High frequency (hourly) variation in vertical distribution and abundance of meroplanktonic larvae in nearshore waters during strong internal tidal forcing. Continental Shelf Research 117:92–99, https://doi.org/​10.1016/j.csr.2016.02.004.

Lucas, A.J., P.J.S. Franks, and C.L. Dupont. 2011. Horizontal internal-tide fluxes support elevated phytoplankton productivity over the inner continental shelf. Limnology and Oceanography: Fluids and Environments 1(1):56–74, https://doi.org/10.1215/21573698-1258185.

Lucas, A.J., J.D. Nash, R. Pinkel, J.A. MacKinnon, A. Tandon, A. Mahadevan, M.M. Omand, M. Freilich, D. Sengupta, M. Ravichandran, and A. Le Boyer. 2016. Adrift upon a salinity-​stratified sea. Oceanography 29(2):134–145, https://doi.org/​10.5670/oceanog.2016.46.

Macías, D., R. Somavilla, J.I. González-Gordillo, and F. Echevarría. 2010. Physical control of zooplankton distribution at the Strait of Gibraltar during an episode of internal wave generation. Marine Ecology Progress Series 408:79–85, https://doi.org/​10.3354/​meps08566.

MacKinnon, J.A., and M.C. Gregg. 2003. Mixing on the late-summer new England shelf—​solibores, shear, and stratification. Journal of Physical Oceanography 33(7):1,476–1,492, https://doi.org/10.1175/1520-0485(2003)033​<1476:MOTLNE>2.0.CO;2.

McPhee-Shaw, E.E., D.A. Siegel, L. Washburn, M.A. Brzezinski, J.L. Jones, A. Leydecker, and J. Melack. 2007. Mechanisms for nutrient delivery to the inner shelf: Observations from the Santa Barbara Channel. Limnology and Oceanography 52(5):1,748–1,766, https://doi.org/​10.4319/lo.2007.52.5.1748.

Moore, S.E., and R.C. Lien. 2007. Pilot whales follow internal solitary waves in the South China Sea. Marine Mammal Science 23(1):193–196, https://doi.org/​10.1111/​j.1748-7692.2006.00086.x.

Muacho, S., J.C.B. Da Silva, V. Brotas, and P.B. Oliveira. 2013. Effect of internal waves on near-surface chlorophyll concentration and primary production in the Nazaré Canyon (west of the Iberian Peninsula). Deep-Sea Research Part I 81:89–96, https://doi.org/10.1016/​j.dsr.2013.07.012.

Nash, C.E., C.M. Kuo, and S.C. McConnel. 1974. Operational procedures for rearing larvae of the grey mullet (Mugil cephalus L.). Aquaculture 3:15–24, https://doi.org/​10.1016/​0044-8486(74)90095-7.

Nash, C.E., C.M. Kuo, W.D. Madden, and C.L. Paulsen. 1977. Swim bladder inflation and survival of Mugil cephalus to 50 days. Aquaculture 12:89–94, https://doi.org/10.1016/0044-8486(77)90049-7.

Nash, J., E. Shroyer, S. Kelly, and M. Inall. 2012. Are any coastal internal tides predictable? Oceanography 25(2):80–95, https://doi.org/​10.5670/oceanog.2012.44.

Navarro, M.O., G.T. Kwan, O. Batalov, C.Y. Choi, N.T. Pierce, and L.A. Levin. 2016. Development of embryonic market squid, Doryteuthis opalescens, under chronic exposure to low environmental pH and [O₂]. PLoS ONE 11(12):1–17, https://doi.org/​10.1371/​journal.pone.0167461.

Oliver, R.L. 1994. Floating and sinking in gas-​vacuolate cyanobacteria. Journal of Phycology 30(2):161–173, https://doi.org/​10.1111/j.0022-3646.1994.00161.x.

Omand, M.M., J.J. Leichter, P.J.S. Franks, R.T. Guza, A.J. Lucas, and F. Feddersen. 2011. Physical and biological processes underlying the sudden surface appearance of a red tide in the nearshore. Limnology and Oceanography 56(3):787–801, https://doi.org/10.4319/lo.2011.56.3.0787.

Pan, X., G.T.F. Wong, F.K. Shiah, and T.Y. Ho. 2012. Enhancement of biological productivity by internal waves: Observations in the summertime in the northern South China Sea. Journal of Oceanography 68(3):427–437, https://doi.org/​10.1007/s10872-012-0107-y.

Paulson, C.A., and J.J. Simpson. 1977. Irradiance measurements in the upper ocean. Journal of Physical Oceanography 7(6):952–956, https://doi.org/​10.1175/1520-0485(1977)007​<0952:imituo>2.0.co;2.

Pineda, J. 1994. Internal tidal bores in the nearshore: Warm-water fronts, seaward gravity currents and the onshore transport of neustonic larvae. Journal of Marine Research, 52(3):427–458, https://doi.org/​10.1357/0022240943077046.

Pineda, J. 1999. Circulation and larval distribution in internal tidal bore warm fronts. Limnology and Oceanography 44(6):1,400–1,414, https://doi.org/​10.4319/lo.1999.44.6.1400.

Reid, E.C., T.M. DeCarlo, A.L. Cohen, G.T.F. Wong, S.J. Lentz, A. Safaie, A. Hall, and K.A. Davis. 2019. Internal waves influence the thermal and nutrient environment on a shallow coral reef. Limnology and Oceanography 64(5):1,949–1,965, https://doi.org/​10.1002/lno.11162.

Richards, C., D. Bourgault, P.S. Galbraith, A. Hay, and D.E. Kelley. 2013. Measurements of shoaling internal waves and turbulence in an estuary. Journal of Geophysical Research 118(1):273–286, https://doi.org/​10.1029/2012JC008154.

Ruvalcaba-Aroche, E.D., A. Filonov, L. Sánchez-Velasco, L.B. Ladah, and J. Cruz-Hernández. 2019. Internal tidal waves in Tiburon Basin (Gulf of California, Mexico) modulate fish larvae aggregations. Continental Shelf Research 178(1):41–50, https://doi.org/10.1016/j.csr.2019.03.012.

Sandstrom, H., and J.A. Elliott. 1984. Internal tide and solitons on the Scotian Shelf: A nutrient pump at work. Atlantic 89(4):6,415–6,426, https://doi.org/​10.1029/JC089iC04p06415.

Shanks, A.L. 1983. Surface slicks associated with tidally forced internal waves may transport pelagic larvae of benthic invertebrates and fishes shoreward. Marine Ecology Progress Series 13:311–315, https://doi.org/10.3354/meps013311.

Shanks, A.L. 1987. The onshore transport of an oil spill by internal waves. Science 235(4793):1,198–1,200, https://doi.org/10.1126/science.235.4793.1198.

Shanks, A.L. 1988. Further support for the hypothesis that internal waves can cause shoreward transport of larval invertebrates and fish. Fishery Bulletin 86(4):703–714.

Shanks, A.L. 1995. Orientated swimming by megalopae of several eastern North Pacific crab species and its potential role in their onshore migration. Journal of Experimental Marine Biology and Ecology 186(1):1–16, https://doi.org/​10.1016/0022-0981(94)00144-3.

Shanks, A.L., and W.G. Wright. 1987. Internal-wave-mediated shoreward transport of cyprids, megalopae, and gammarids and correlated longshore differences in the settling rate of intertidal barnacles. Journal of Experimental Marine Biology and Ecology 114(1):1–13, https://doi.org/​10.1016/​0022-0981(87)90135-3.

Shroyer, E.L., J.N. Moum, and J.D. Nash. 2010. Vertical heat flux and lateral mass transport in nonlinear internal waves. Geophysical Research Letters 37(8), https://doi.org/10.1029/2010GL042715.

Shroyer, E.L., J.N. Moum, and J.D. Nash. 2011. Nonlinear internal waves over New Jersey’s continental shelf. Journal of Geophysical Research 116(C3), https://doi.org/​10.1029/​2010JC006332.

Sinnett, G., F. Feddersen, A.J. Lucas, G. Pawlak, and E. Terrill. 2018. Observations of nonlinear internal wave run-up to the surfzone. Journal of Physical Oceanography 48:531–554, https://doi.org/10.1175/JPO-D-17-0210.1.

Stastna, M., and K.G. Lamb. 2002. Large fully nonlinear internal solitary waves: The effect of background current. Physics of Fluids 14(9):2,987–2,999, https://doi.org/​10.1063/1.1496510.

Stevick, P.T., L.S. Incze, S.D. Kraus, S. Rosen, N. Wolff, and A. Baukus. 2008. Trophic relationships and oceanography on and around a small offshore bank. Marine Ecology Progress Series 363:15–28, https://doi.org/10.3354/meps07475.

Thomas, J.A., J.A. Lerczak, and J.N. Moum. 2016. Horizontal variability of high-frequency nonlinear internal waves in Massachusetts Bay detected by an array of seafloor pressure sensors. Journal of Geophysical Research 121(8):5,587–5,607, https://doi.org/10.1002/2016JC011866.

Thorpe, S.A. 1968. On the shape of progressive internal waves. Philosophical Transactions of the Royal Society A 263(1145):563–614, https://doi.org/​10.1098/rsta.1968.0033.

Wall, M., L. Putchim, G.M. Schmidt, C. Jantzen, S. Khokiattiwong, and C. Richter. 2015. Large-amplitude internal waves benefit corals during thermal stress. Proceedings of the Royal Society B 282(1799), https://doi.org/10.1098/rspb.2014.0650.

Walter, R.K., C.B. Woodson, P.R. Leary, and S.G. Monismith. 2014. Connecting wind-driven upwelling and offshore stratification to nearshore internal bores and oxygen variability. Journal of Geophysical Research 119:3,517–3,534, https://doi.org/​10.1002/2014JC009998.

Wang, Y.H., C.F. Dai, and Y.Y. Chen. 2007. Physical and ecological processes of internal waves on an isolated reef ecosystem in the South China Sea. Geophysical Research Letters 34(18), https://doi.org/​10.1029/2007GL030658.

Wishner, K.F., D.M. Outram, B.A. Seibel, K.L. Daly, and R.L. Williams. 2013. Zooplankton in the eastern tropical north Pacific: Boundary effects of oxygen minimum zone expansion. Deep Sea Research Part I 79:122–140, https://doi.org/10.1016/​j.dsr.2013.05.012.

Witman, J.D., J.J. Leichter, S.J. Genovese, and D.A. Brooks. 1993. Pulsed phytoplankton supply to the rocky subtidal zone: Influence of internal waves. Ecology 90:1,686–1,690, https://doi.org/​10.1073/​pnas.90.5.1686.

Woodson, C.B. 2018. The fate and impact of internal waves in nearshore ecosystems. Annual Review of Marine Science 10(1):421–441, https://doi.org/​10.1146/annurev-marine-121916-063619.

Zeidberg, L.D., J.L. Butler, D. Ramon, A. Cossio, K.L. Stierhoff, and A. Henry. 2012. Estimation of spawning habitats of market squid (Doryteuthis opalescens) from field surveys of eggs off Central and Southern California. Marine Ecology 33(3):326–336, https://doi.org/​10.1111/​j.1439-0485.2011.00498.x.

Zeldis, J.R., and J.B. Jillett. 1982. Aggregation of pelagic Munida gregaria (Fabricius) (Decapoda, Anomura). Journal of Plankton Research 4(4):839–857, https://doi.org/10.1093/plankt/4.4.839.

Zhang, S., M.H. Alford, and J.B. Mickett. 2015. Characteristics, generation and mass transport of nonlinear internal waves on the Washington continental shelf. Journal of Geophysical Research 120:741–758, https://doi.org/​10.1002/2014JC010393.

Zimmerman, R.C., and J.N. Kremer. 1984. Episodic nutrient supply to a kelp forest ecosystem in Southern California. Journal of Marine Research 42(3):591–604, https://doi.org/​10.1357/​002224084788506031.

This is an open access article made available under the terms of the Creative Commons Attribution 4.0 International License (https://creativecommons.org/licenses/by/4.0/), which permits use, sharing, adaptation, distribution, and reproduction in any medium or format as long as users cite the materials appropriately, provide a link to the Creative Commons license, and indicate the changes that were made to the original content. Images, animations, videos, or other third-party material used in articles are included in the Creative Commons license unless indicated otherwise in a credit line to the material. If the material is not included in the article’s Creative Commons license, users will need to obtain permission directly from the license holder to reproduce the material.